Содержание
- Введение (3),
- Эффект безопорного движения (3),
- Силы в потенциальном течении (4),
- Опорное движение (5),
- Безопорное движение электропроводящего магнита с током (8),
- Движение соленоида с током и униполярный двигатель Фарадея (9),
- Симметричные и асимметричные деформации электромагнитных полевых объектов (10),
- Заключение (11),
- Литература (11).
Введение
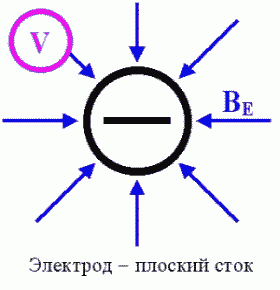
В аксиоматике энергетического поля электрический ток, магнитные и электростатические поля рассматриваются в виде полевых объектов, отличающихся только картиной течений и их пространственных конфигураций [1], [2], [3]. Магнит, как полевой объект, сопоставляется с пространственным диполем (илл. IV). Магнитный поток B движется по образующей тора. Электростатическое поле, как полевой объект, например, положительно заряженный электрод, с центральной или осевой симметрией, сопоставляется соответственно с пространственным или плоским стоком с центрально-радиальным движением потока BE (илл. V). Электрический ток - как объект полевой вихревой структуры, сопоставляется с вихревым винтовым движением, например, вдоль проводника, между полевыми объектами (заряженными телами) с различными потенциалами (илл. VI). При этом осевая составляющая движения интерпретируется как собственно электрический ток J, а окружная составляющая - как сопутствующий току магнитный поток BJ.


Вышеприведенных представлений о полевых объектах нам вполне достаточно для выяснения природы опорного и безопорного движения.
Эффект безопорного движения
Впервые эффект безопорного движения был обнаружен экспериментально в опыте Фарадея с униполярным двигателем. Униполярный двигатель Фарадея представляет собой электропроводящий магнитный диск, свободно насаженный на ось (илл. I). При формировании радиального тока J путем подачи разности потенциалов между ободом и осью наблюдается самопроизвольное непрерывное вращение диска при отсутствии внешних опорных сил. До сих пор не было дано физического объяснения данного эффекта.

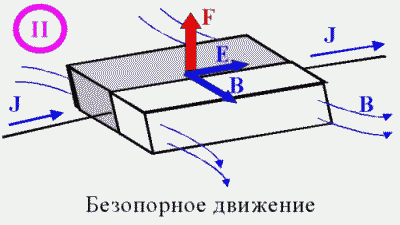
Эффект безопорного движения наблюдается и для плоского токопроводящего магнита с током (илл. II). Сила безопорного движения ортогональна плоскости, построенной на электрическом E и магнитном B векторах. Как и в опыте Фарадея, природа этой силы так и не была выяснена.
Наличие безопорного движения зафиксировано в опыте Сигалова. Обнаружено поступательное движение соленоида с током при взаимодействии его с собственным прямолинейным участком тока (илл. III). Объяснение автора основывается на эффекте самодействия. Физические основы данного эффекта до сих пор не известны.

Силы в потенциальном течении
По результатам первоначальных исследований электрических и магнитных полей Фарадей и Максвелл пришли к выводу о физической реальности электрических и магнитных линий тока. В дальнейшем их физическое существование было поставлено под сомнение. Это связано с тем, что любое движение сопоставлялось с эффектом проявления силы. Это означает, что в магнитном поле при наличии движения должна фиксироваться сила. Опыт же свидетельствует, что на тела в магнитном поле никакая сила не действует. Отсюда был сделан вывод об отсутствии какого-либо движения в магнитном поле и о том, что никакие физические линии тока не существуют.
В действительности сопоставлять движение с обязательным проявлением силы неправомерно. Исследуя свойства потенциального течения, приходим к выводу, что в любой точке потенциального течения проявление сил отсутствует [4]. Так, например, шар не испытывает никакого сопротивления со стороны равномерно поступательного движения жидкости. Этот результат резко противоречит данным опыта и носит название парадокса Эйлера-Даламбера. С одной стороны, он объясняется тем, что в действительности безотрывное безвихревое обтекание шара не имеет места; с поверхности шара срываются вихри, которые видоизменяют как картину течения, так и распределение давления по поверхности шара. С другой стороны - отсутствием градиента потенциала в потенциальном течении, наличие которого и определяет существование силы [1].
Несмотря на то, что физические представления о натяжении и боковом давлении электрических и магнитных линий, введенные Фарадеем и Максвеллом, на сегодняшний день считаются абстрактными [5] “линии напряженности и индукции есть геометрический образ, введенный для графического изображения полей”, тем не менее, представления Фарадея и Максвелла оказались весьма полезны, так как позволяют просто определить характер механических сил в электромагнитном поле. Рассмотрим в качестве примера прямой ток в однородном магнитном поле (илл. VII). Линии индукции поля В до внесения тока имеют вид параллельных прямых линий, направленных слева направо. Линии же тока представляют собой концентрические окружности. Складываясь, оба поля дают картину линий, изображенную на илл., откуда сразу можно заключить, что на провод действует сила, перпендикулярная к проводу и к первоначальному магнитному полю.
Опорное движение

Вначале рассмотрим причину возникновения опорного движения и дадим его определение на примере взаимодействия тока с магнитным полем (илл. VIII). В межполюсном пространстве магнита NS картина линий тока соответствует случаю потенциального течения от северного полюса магнита N к южному S. При введении в потенциальный поток вихревого потока, создаваемого линией тока J, протекающего по проводнику 1, получим картину течения, очень близкую к картине потенциального обтекания цилиндра с циркуляцией. Такое течение дает большую поперечную силу. Это явление известно под названием эффекта Магнуса, оно проявляется, в частности, при игре в теннис в тех случаях, когда мяч получает срезывающий удар.

На илл. IX изображена картина течения около вращающегося цилиндра [6]. На его верхней стороне, где течение жидкости и вращение стенки направлены в одну и ту же сторону, плотность линий тока значительно больше, чем на нижней стороне, где течение жидкости и вращение стенки цилиндра направлены в противоположные стороны. Градиент плотностей линий тока и является причиной возникновения большой поперечной силы F. Из подобия картин течения около проводника с током и около вращающегося цилиндра, которые близки к картине потенциального обтекания цилиндра с циркуляцией, мы можем сделать вывод о том, что в этих случаях возникновение силы связано с эффектом Магнуса.
На илл. VIII магнит 1 и ток 2 (илл. X) представлены в виде полевых объектов. Картина линий тока полевого объекта (магнита) 1 близка к картине тока диполя, а картина линий тока, создаваемая проводником с током 2 - картине циркуляции. Внедрение полевого объекта 2 в полевой объект 1 приводит к деформации линий тока последнего. Степень деформации мы можем отобразить графически в виде "густоты" линий тока (илл. X,а), а качественно - в виде "динамической плотности" линий тока r (илл. X,б), где r ¥ - фоновая динамическая плотность линий тока на бесконечном удалении от полевого объекта 1. Введение динамической плотности дает нам возможность рассматривать возникновение сил в области полевого объекта таким же образом, как это принято в современной физике. Поэтому мы можем говорить, что причина возникновения силы в области двух полевых объектов вызвана градиентом динамического давления D r , в нашем случае - между верхней и нижней частью полевого объекта 2.
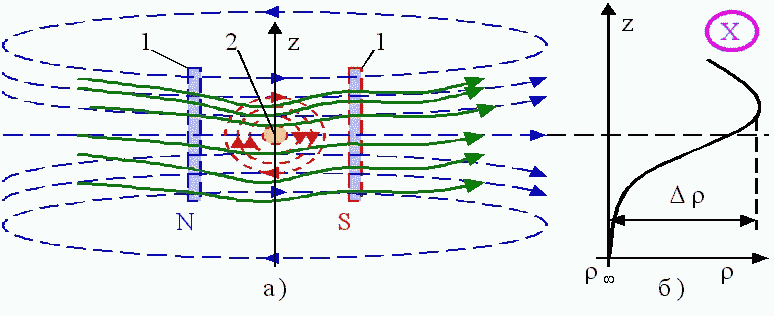
Так как градиент динамической плотности создается в теле полевого объекта 1, то мы будем считать его опорным, относительно которого сила действует на тело полевого объекта 2. При наличии в этом случае движения, данное движение будем называть опорным.
Опорное движение, связанное с эффектом Магнуса, проявляется в различных физических эффектах, например, в интегральном электромагнитогидродинамическом эффекте, который заключается в возникновении вихревого движения электропроводной среды (в частности - жидкости), находящейся в магнитном поле при протекании через нее электрического тока. Иллюстрирует действие магнитного поля, согласно правилу левой руки, не только на электронный ток в проводнике, но и на ионный ток в электролите[7]. Формулируется эффект так: "При протекании электрического тока в среде, находящейся в магнитном поле, в зоне коаксиально расположенных электродов возникает вихревое движение среды, охватывающее центральный электрод, обусловленное появлением момента силы, с направлением вектора скорости вихревого движения перпендикулярно вектору магнитной индукции".
Описание эффекта проведем на примере электропроводной жидкости. Кювета с электропроводной жидкостью помещается в магнитном поле, вектор магнитной индукции которого направлен вертикально. В центральной части кюветы в жидкость опущен электрод. Второй периферийный электрод выполнен кольцевым и установлен по периметру кюветы. При формировании линий тока в электропроводной жидкости наблюдается вихревое движение жидкости в зоне между центральным и периферийным электродами с центром вихря в зоне центрального электрода. Частота вращения максимальна в центре и уменьшается при удалении от центрального электрода.
Схема эксперимента представлена на илл. XI. На илл. изображены: 1 - сосуд, 2 - расплавленный металл, 3 - спиральная катушка (электромагнит), 4 - металлическое кольцо, 5 - электрод. В качестве электропроводной жидкости в эксперименте использовалось олово. Сосуд с расплавленным оловом помещен в магнитное поле, вектор магнитной индукции которого направлен вертикально. На илл. обозначены: "" - южный магнитный полюс, "" - северный магнитный полюс. При подключении напряжения расплавленный металл приходит в движение. Наблюдается вихревое движение расплавленного олова при значении тока, начиная от 5-6 А. Направление движения показано стрелкой. При дальнейшем увеличении тока интенсивность вихревого движения возрастает, что приводит к образованию глубокой воронки в центре сосуда. При изменении направления магнитного поля или при изменении полярности приложенного напряжения направление вихревого движения меняется на противоположное.
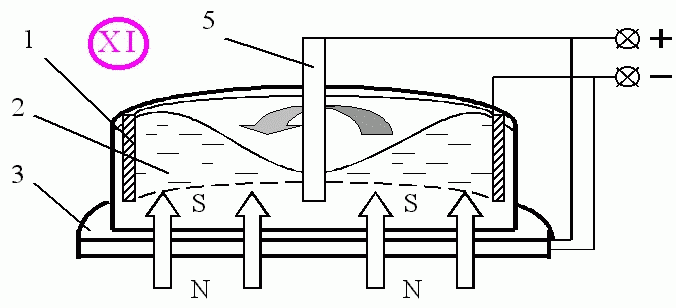
Опорным телом здесь является полевой объект - магнит, а сила приложена к полевому объекту 2 - расплавленному металлу, включащему в себя вихревые линии электрического тока.
Безопорное движение электропроводящего магнита с током
Рассмотрим безопорное движение на примере электропроводящего магнита с током. Предположим, что магниту (первичному полевому объекту) придана цилиндрическая форма, а направление движения магнитного потока В ортогонально оси цилиндра (илл. XII).
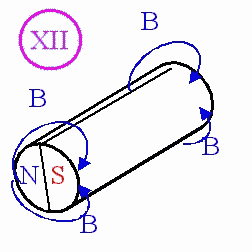
Пропускание электрического тока по оси магнита приводит к формированию вторичного полевого объекта с вихревой винтовой структурой линий тока и к совмещению двух полевых объектов в один (илл. XIII,а). При этом плотность линий тока в верхней и нижней частях совмещенного полевого объекта будет различной (илл. XIII,б). В верхней части - r >>r ¥ , в нижней части - r ® r ¥ , где r ¥ - фоновая динамическая плотность на бесконечном удалении от полевого объекта. Градиент плотностей линий тока D r в динамическом пограничном слое совмещенного полевого объекта приводит к возникновению нескомпенсированной силы F, воздействующей на физическое тело совмещенного полевого объекта, что и является причиной его движения без внешней опоры. В качестве опоры выступает само тело первичного полевого объекта (илл. XII), заполняющее все окружающее пространство. Другими словами, мы имеем дело с деформацией полевого объекта, т.е. неравномерным распределением плотностей линий тока в ограниченной области пространства. Процесс выравнивания градиента плотностей сопровождается эффектом движения. Данный эффект мы будем называть безопорным движением.

Сформулируем обратную задачу, т.е. определим, какие условия необходимы для создания безопорного движения? Исходя из изложенного, мы можем датьследующее определение: для создания безопорного движения необходимо выполнить условие градиента плотности линий тока в динамическом пограничном слое совмещенного полевого объекта или в динамическом пограничном слое системы полевых объектов.
В качестве примеров эффекта безопорного движения рассмотрим поступательное движение соленоида с током при взаимодействии его с собственным прямолинейным участком тока и униполярный двигатель Фарадея.
Движение соленоида с током и униполярный двигатель Фарадея
Эффект безопорного движения соленоида с током установлен в опыте Р. Сигалова [8] (илл. III). Здесь мы, как и в предыдущем случае, имеем дело с совмещенным полевым объектом, создаваемым определенной пространственной конфигурацией проводника с током. Первичным объектом мы будем считать магнитное поле B, создаваемое окружным витком тока, а вторичным - вихревое винтовое движение BJ, создаваемое линейным током. Картина течений, создаваемая окружным и линейным током показана на илл. XIV,a. Здесь точкой показано движение к наблюдателю, а крестиком - от наблюдателя. Так как количество линий тока, создаваемых окружным током внутри кольца тока равно тому же их количеству снаружи кольца, а плотность линий тока, создаваемая линейным током, максимальна в непосредственной близости от линейного тока, то максимальный градиент плотностей линий тока совмещенного полевого объекта будет в его центре, как показано на илл. XIV,б. Наличие градиента динамического давления в центре совмещенного полевого объекта приводит к возникновению безопорной силы F, стремящейся скомпенсировать деформацию полевого объекта.

Тот же процесс деформации полевого объекта в области линейного тока в эксперименте Фарадея с униполярным двигателем приводит к локальной безопорной силе, приводящей к эффекту вращения дискового магнита с радиальным током (илл. I).
Симметричные и асимметричные деформации электромагнитных полевых объектов
Рассматривая физику опорных и безопорных движений, мы пришли к понятию деформации полевого объекта. Методологически более правильно рассматривать силы не как результат какого либо движения, а как результат устранения деформации полевого объекта. С этой точки зрения мы можем ввести понятие симметричных и асимметричных безопорных сил, т.е. сил, направленных на устранение деформации полевого объекта. Примеры некоторых асимметричных сил мы уже рассмотрели. Это опорные силы для проводника с током в магнитном поле, которые стремятся устранить деформацию первичного полевого объекта - магнитного поля, создаваемую вторичным полевым объектом, т.е. вихревым винтовым движением в области проводника с током. Это безопорные силы для совмещенных электромагнитных объектов, таких как электропроводящий магнит с током и соленоид с током, стремящиеся устранить деформацию совмещенной электромагнитной системы полевых объектов и приводящих к безопорному движению.
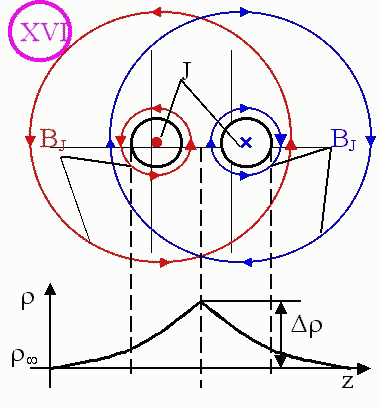
Наряду с асимметричной деформацией полевых объектов существует и симметричная деформация. Одним из примеров такой деформации является взаимодействие двух линейных токов. Из опыта следует, что параллельные токи "притягиваются", а противоположные - отталкиваются. Рассмотрим физику этого процесса. На илл. XV показана картина течения для совмещенного полевого объекта, создаваемого двумя параллельными токами, а на илл. XVI - встречными токами.
В случае параллельных токов в центре системы двух полевых объектов находится зона пониженной динамической плотности, что говорит о симметричной деформации совмещенного полевого объекта. Поэтому сила, стремящаяся компенсировать центрально-симметричную деформацию, направлена от периферии к центру совмещенного полевого объекта и является силой сжатия, которая проявляется в виде взаимного притяжения проводников с током.
В случае встречных токов в центре системы двух полевых объектов находится зона повышенной динамической плотности, что также говорит о симметричной деформации совмещенного полевого объекта. В этом случае сила, стремящаяся компенсировать центрально-симметричную деформацию, направлена от центра к периферии совмещенного полевого объекта и является силой растяжения, которая проявляется в виде взаимного отталкивания проводников с током.

Заключение
Исследование опорных и безопорных движений привело нас к определению понятий симметричной и асимметричной деформации системы полевых объектов, к отображению величины деформации градиентом динамической плотности линий тока. При этом проявление сил сопоставляется не с эффектом движения, а с результатом деформации системы полевых объектов. Результаты приведенных здесь исследований мы можем распространить на все микро и макро полевые объекты, отображающие физические тела и системы тел в силу электромагнитной природы атомов и молекул в них входящих.

Литература
- Балабай В. И. Фундаментальное энергетическое поле. Физико-математическая модель единого поля-материи. Элементы энергетической физики. Книга подготовлена к печати.
- Балабай В. И., Иванько Ю. В., Шаповаленко В. В. Элементы энергетической физики. 2004 г. Статья подготовлена к публикации.
- Балабай В. И. Природа гравитации. 2004 г. Статья подготовлена к публикации.
- Лаврентьев М. А. И Шабат Б.В. Методы теории функции комплексного переменного. М-Л.: Изд-во технико-теоретич. л-ры, 1951. – 606 с.
- Калашников С. Г., Электричество, “Наука”, 1970.
- Шлихтинг Г. Теория пограничного слоя. Пер. с нем. М.: Изд. "Наука", гл. ред. физ.-мат. л- ры, 1969. С - 742.
- Косинов Н. В., Гарбарук В. И., Косинов Л. В. Лабораторные эксперименты, объясняющие механизм вращения Земли. /ж. Физический вакуум и природа/, №5, 2002 г. с. 138-142.
- Сигалов Р. Т., Шаповалова Т. И., Каримов Х. Х., Самсонов Н. И. Новые исследования движущих сил магнитного поля. - Ташкент: ФАН, 1975.
УДК 52.539.12; 524.8; 530.12; 531.51; 537; 537.8
Дата публикации: Прочитано: 35093 раз